总结一下广度优先搜索的原理和用法。
引子
先看这道题104. 二叉树的最大深度,题目中给出一个二叉树,求这个二叉树的最大深度。例子中给出下面的二叉树
1
2
3
4
5
|
3
/ \
9 20
/ \
15 7
|
这个如何解决呢?肉眼可见,最大深度是3。
构建二叉树
首先为了便于调试,需要构建一颗二叉树,题目中的给出的是二叉树的层序遍历的结果,我们用INT_MAX代替null,使用如下函数构造二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
void ConstructBinTree(vector<int> &nodes, TreeNode *root)
{
if (nodes.size() == 0 || nodes[0] == INT_MAX)
{
root = nullptr;
return;
}
queue<TreeNode *> iq;
int id = 0;
root->val = nodes[id++];
iq.emplace(root);
while (!iq.empty() && id < nodes.size())
{
TreeNode *node = iq.front();
iq.pop();
// check vectors for left node
if (nodes[id] != INT_MAX)
{
TreeNode *leftNode = new TreeNode;
leftNode->val = nodes[id];
node->left = leftNode;
iq.emplace(leftNode);
}
else
{
node->left = nullptr;
}
id++;
// add right node
if (nodes[id] != INT_MAX)
{
TreeNode *rightNode = new TreeNode;
rightNode->val = nodes[id];
node->right = rightNode;
iq.emplace(rightNode);
}
else
{
node->right = nullptr;
}
id++;
}
return;
}
|
下面是中序遍历二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void ScanBinMiddle(TreeNode *tree)
{
if (tree == nullptr)
{
return;
}
// handle value
cout << tree->val << " ";
if (tree->left)
{
ScanBinMiddle(tree->left);
}
if (tree->right)
{
ScanBinMiddle(tree->right);
}
}
|
递归解法
二叉树的比较普遍的解法是使用递归,我们需要找出递归的关系式,然后用程序写出来。递归解决问题的思路包括下面两点
描述变量
我们有一个关于目标变量的描述,在这个题目中目标变量是整棵树的最大深度,放弃整体的概念,假设你站在根节点往下看,会看到它有左右两个子树,每棵树又有自己的节点和深度。所以假定推导的变量是
maxdepth[node]表示以node为根节点的树的最大深度
递归关系式
查看这个值和左右子树的关系是什么?3这个node的最大深度是9这个node最大深度和20这个node的最大深度的最大值 + 1,重新表述下就是下面的关系式maxD[node] = max(maxD[node->left], maxD[node->right]) + 1。
终止条件
终止条件比较简单,在访问到null节点的时候返回0即可,因为以这个节点为根的树是不存在的,所以深度为0。于是有下面的代码
1
2
3
4
5
6
7
8
9
|
int maxDepth(TreeNode* root)
{
// 终止条件
if (root == nullptr) {
return 0;
}
// 关系式
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
|
广度优先搜索算法(BFS)
不使用递归,还有另一种解法,一层层观察整棵树,第一层1个节点,第二层2个节点,第三层2个节点。每一层的节点之间使用左右子树联系起来,所以根据第1层的节点可以访问第2层的节点,根据第2层的节点可以访问第3层的节点,所以可以这么做。记录整棵树最深的深度是maxdepth = 0,
- 访问第一层的根节点,如果非空则
maxdepth++,否则返回;
- 查看第一层的根节点是否有左右子树,有的话再分别访问左子树和右子树,
maxdepth++;
- 循环步骤2,直到所有的节点都被访问到。
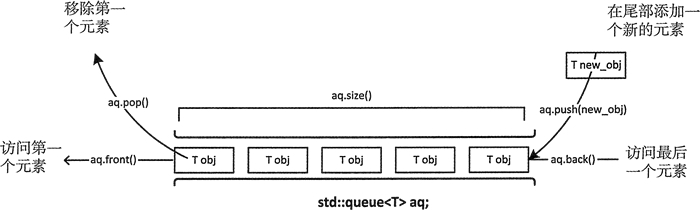
这里可以使用队列保存需要被访问的节点,如下图所示,分别在头和尾弹出和插入节点,
结合上面的步骤,depth = 1,将root的根节点添加到队列结尾
- 我们一次将一层的节点放入到队列中;
- 判断当前队列是否为空。
- 如果当前的队列不为空,那么将队列中的每个节点pop出来之后再考察这个节点的左右子树,如果有就将它们插入到队列的尾巴,
depth++;
- 如果当前队列为空,return
所以有了下面的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
int maxDepth(TreeNode* root)
{
// 如果为空,那么返回0
if (root == nullptr) {
return 0;
}
queue<TreeNode *> qu;
int depth = 0;
// 添加根节点
qu.push(root);
while (!qu.empty()) {
int qz = qu.size();
for (int i = 0;i < qz;i++) { // 考察队列中的每个节点,是否有左子树和右子树
TreeNode * node = qu.front();
qu.pop();
// 如果有左右子节点,那么添加到队列中
if (node->left) {
qu.push(node->left);
}
if (node->right) {
qu.push(node->right);
}
}
depth++;
}
return depth;
}
|
下图是资料3中的图示过程,简单明了。
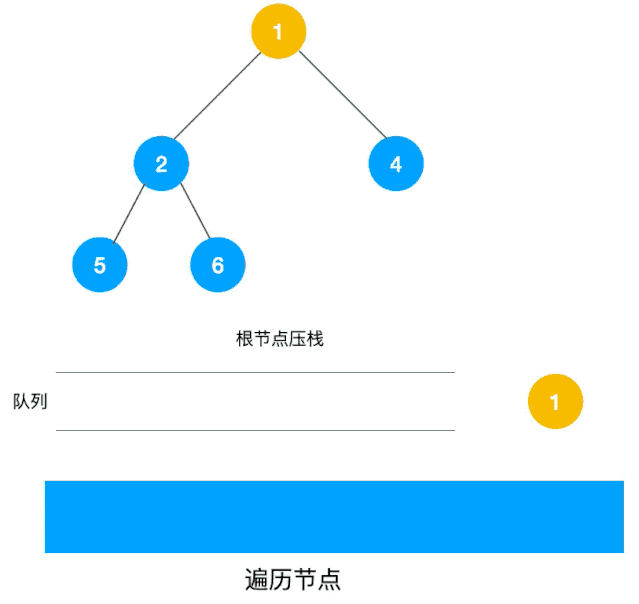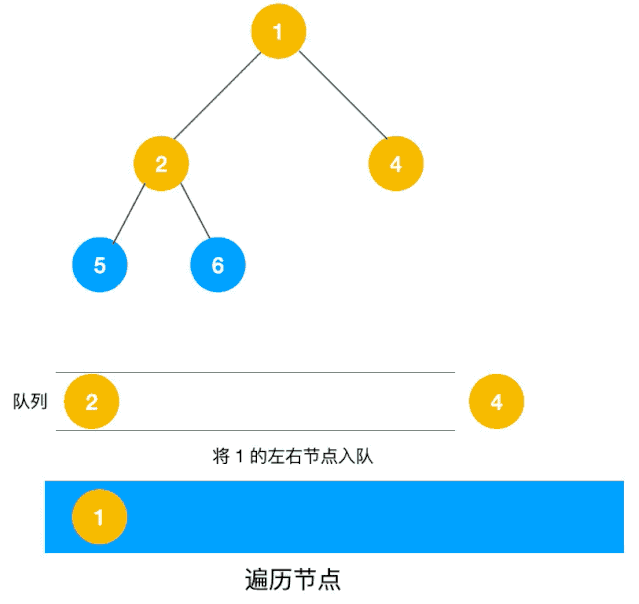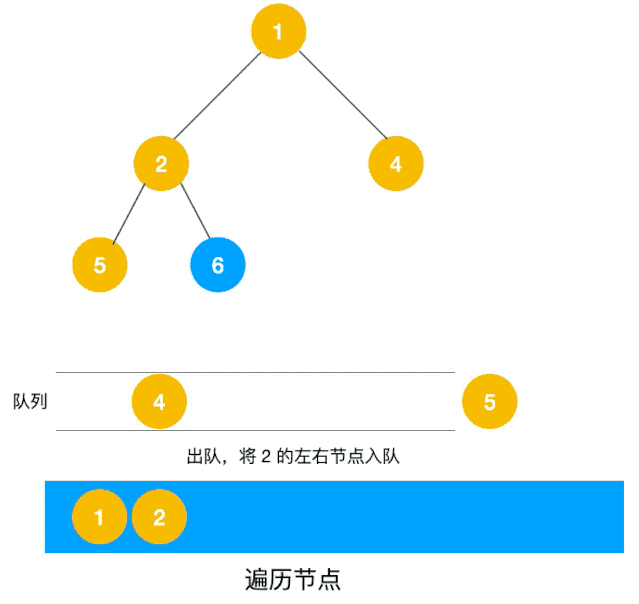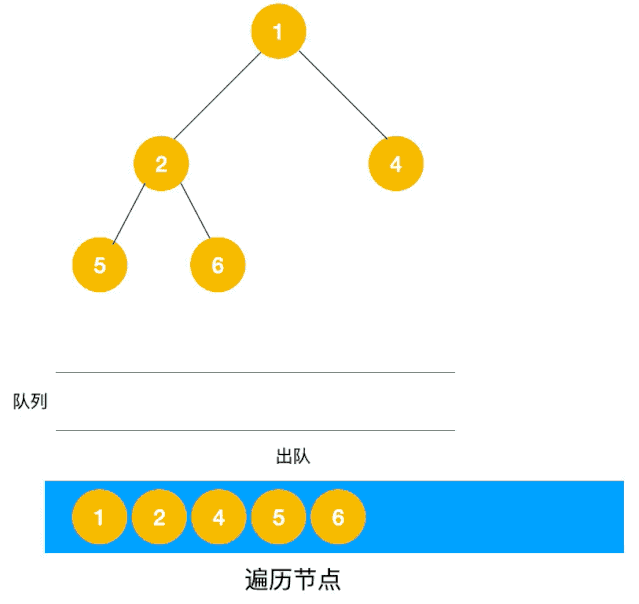
数据结构
队列
使用队列保存每一层的节点,如下图所示,队列是先进先出的数据结构,包括如下的属性和方法
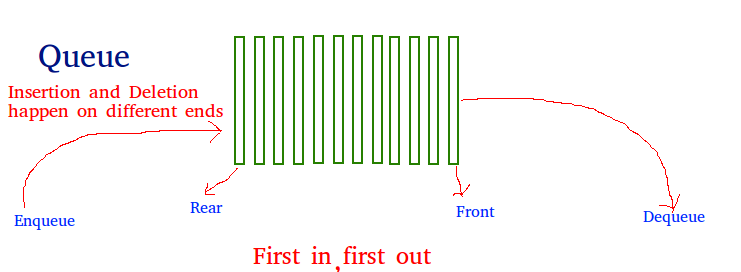
- 队列头(front),表示队列最开始的元素;
- 队列尾(rear),表示队列最后加入的元素;
- 队列长度,当前的队列长度,就是rear - front + 1;
- 出队(pop),队列头弹出,队列长度-1,front++;
- 入队(push),队列尾添加元素,队列长度+1,rear++
STL中的queue
C++的stl使用queue表示队列,常用的操作和属性如下表所示
front():返回 queue 中第一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的。back():返回 queue 中最后一个元素的引用。如果 queue 是常量,就返回一个常引用;如果 queue 为空,返回值是未定义的。push(const T& obj):在 queue 的尾部添加一个元素的副本。这是通过调用底层容器的成员函数 push_back() 来完成的。push(T&& obj):以移动的方式在 queue 的尾部添加元素。这是通过调用底层容器的具有右值引用参数的成员函数 push_back() 来完成的。pop():删除 queue 中的第一个元素。size():返回 queue 中元素的个数。empty():如果 queue 中没有元素的话,返回 true。emplace():用传给 emplace() 的参数调用 T 的构造函数,在 queue 的尾部生成对象。swap(queue<T> &other_q):将当前 queue 中的元素和参数 queue 中的元素交换。它们需要包含相同类型的元素。也可以调用全局函数模板 swap() 来完成同样的操作。
典型的使用方法如下,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// CPP program to illustrate
// Application of push() and pop() function
#include <iostream>
#include <queue>
using namespace std;
int main()
{
int c = 0;
// Empty Queue
queue<int> myqueue;
myqueue.push(5);
myqueue.push(13);
myqueue.push(0);
myqueue.push(9);
myqueue.push(4);
// queue becomes 5, 13, 0, 9, 4
// Counting number of elements in queue
while (!myqueue.empty()) {
myqueue.pop();
c++;
}
cout << c;
}
|
典型题目
二叉树的右视图
题目链接见199. 二叉树的右视图 - 力扣(LeetCode),如果有了上面题目的框架,这个题目其实很简单,既然每次遍历队列保存的这一层所有节点,而且节点的顺序是从左到右保存的,所以可以在每一层遍历的时候将队列的最后一个node加入到这个vector中,代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
vector<int> rightSideView(TreeNode* root)
{
vector<int> rlt;
// empty rlt for empty tree
if (root == nullptr) {
return rlt;
}
queue<TreeNode *> qu;
qu.push(root);
while (!qu.empty()) {
int qz = qu.size();
// add the last node in the current queue
rlt.emplace_back(qu.back()->val);
// add nodes of next layer into the queue
for (int i = 0;i < qz;i++) {
TreeNode * node = qu.front();
qu.pop();
if (node->left) {
qu.push(node->left);
}
if (node->right) {
qu.push(node->right);
}
}
}
return rlt;
}
|
二叉树中所有距离为 K 的结点
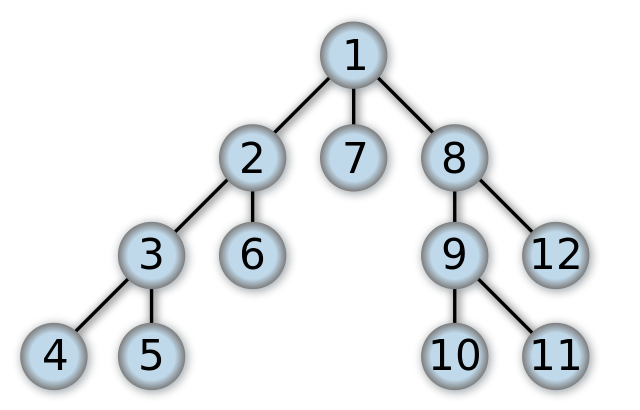
题目见863. 二叉树中所有距离为 K 的结点 - 力扣(LeetCode),这道题稍微有点复杂,观察给出的例子(如下图),与5的节点距离为2的节点除了4和7之外还有1,如果仅仅给出4和7是比较简单的,只要以5为根节点,记录depth = 1,套用引子中的程序,将depth = K + 1的所有的节点列出来即可。
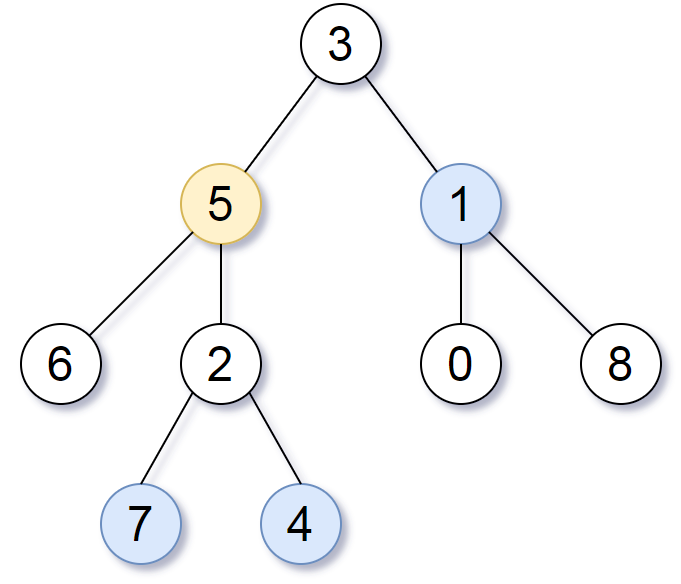
但是往上回溯比较难,换一个思路,我们遍历整个二叉树,
- 记录每个节点的
father节点,left节点和right节点,将二叉树变成图,表示A与这3个节点的任意一个都是连通的;
- 初始化目标节点的
depth = 1,以该节点为圆心,遍历所有的节点,打印出来所有depth = K + 1的节点
第2步实际上是对BFS算法的升维,将二叉树转换为图,代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
|
vector<int> distanceK(TreeNode *root, TreeNode *target, int K)
{
unordered_map<TreeNode *, TreeNode *> umap;
vector<int> rlt;
if (root == nullptr || target == nullptr)
{
return rlt;
}
/************ PART 1 ************/
// find the father node of all the nodes in the tree
queue<TreeNode *> qu;
umap[root] = nullptr;
qu.push(root);
while (!qu.empty())
{
int qz = qu.size();
for (int i = 0; i < qz; i++)
{
TreeNode *node = qu.front();
qu.pop();
if (node->left)
{
qu.push(node->left);
// father node
umap[node->left] = node;
}
if (node->right)
{
qu.push(node->right);
// father node
umap[node->right] = node;
}
}
}
/************ PART 2 ************/
// find the node with depth of K
queue<TreeNode *> newQ;
int depth = 0;
unordered_map<TreeNode *, bool> usedmap;
usedmap[target] = true;
newQ.emplace(target);
while (!newQ.empty() && depth <= K)
{
int qz = newQ.size();
for (int i = 0; i < qz; i++)
{
TreeNode *node = newQ.front();
usedmap[node] = true;
newQ.pop();
if (depth == K)
{
rlt.emplace_back(node->val);
continue;
}
if (node->left && (usedmap.count(node->left) == 0))
{
newQ.push(node->left);
}
if (node->right && (usedmap.count(node->right) == 0))
{
newQ.push(node->right);
}
if (umap[node] != nullptr && (usedmap.count(umap[node]) == 0))
{
newQ.push(umap[node]);
}
}
depth++;
}
//BFS for final rlt
return rlt;
}
|
这个程序分为前后两大部分,
- 第一部分遍历二叉树的每一个节点,记录每个节点的父节点,这里我们使用了哈希表来保存每个节点和它的父节点;
- 第二部分就是核心代码,以target为圆心,将二叉树当作图来遍历,如果这个node有左右节点或者父节点,则表示它跟其他的节点之间联通,则使用BFS算法访问整个图网络。这里尤其要注意,遍历图需要标记当前图中的节点是否被访问过,否则会被多次重复遍历而陷入到死循环中,在这个程序里面,使用
usedmap来做这件事,其实也可以使用vector<TreeNode *>来记录。
为了方便调试,再补一个寻找target node的程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
TreeNode *FindTargetNode(TreeNode *root, int targetVal)
{
if (root == nullptr)
{
return nullptr;
}
queue<TreeNode *> qu;
qu.push(root);
while (!qu.empty())
{
int qz = qu.size();
for (int i = 0; i < qz; i++)
{
TreeNode *node = qu.front();
qu.pop();
if (node->val == targetVal)
{
return node;
}
if (node->left)
{
qu.push(node->left);
}
if (node->right)
{
qu.push(node->right);
}
}
}
}
|
颜色交替的最短路径
题目见1129. 颜色交替的最短路径 - 力扣(LeetCode),这道题难度要大一点,但是后面的方法仍然是BFS,代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
class Solution {
enum color {RED, BLUE};
public:
vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& red_edges, vector<vector<int>>& blue_edges) {
// 由于存在自环或者平行边,所以定义哈希表保存每个结点对应的多条边并初始化
unordered_map<int, vector<int>> redGraph;
unordered_map<int, vector<int>> blueGraph;
for (auto& red : red_edges) redGraph[red[0]].push_back(red[1]);
for (auto& blue : blue_edges) blueGraph[blue[0]].push_back(blue[1]);
const int colorNum = 2;
const int maxNode = 100;
// 由于存在环和平行边,用数组 visit[x][y][color]=true 代表从节点x到节点y的且颜色为color的边被访问过,防止重复访问
// 第三维[2]有两维,第0维代表红色是否访问,第1维代表蓝色是否访问
// 所有的点初始化为0代表为被访问过
bool visited[maxNode][maxNode][colorNum];
memset(visited, false, sizeof(visited));
// step用于记录当前的步长,即从节点0到各节点的步长,从0逐渐+1自增
// res代表节点 0 到节点 X 的最短路径的长度,初始化为最大值
int step = 0;
vector<int> res(n, INT_MAX);
// 定义队列进行BFS,并进行初始化,pair<int, int>的意思是 <当前节点, 路径上颜色>
// 队列初始化先进<0, 1>, 再进<0, 0>,即我们先访问蓝色,再访问红色。
queue<pair<int, color>> myQue; // <node, color> means start from node and select the edge with color
myQue.push(make_pair(0, BLUE));
myQue.push(make_pair(0, RED));
while (!myQue.empty())
{
int size = myQue.size();
++step;
for (int i = 0; i < size; i++)
{
// 队首元素出队列,得到其节点,以及颜色
int curNode = myQue.front().first;
int curColor = myQue.front().second;
myQue.pop();
//若当前已访问的为蓝色边,希望下一个节点的边是红色;反之亦然
if (curColor == BLUE)
{
// 遍历当前节点每一个相邻的节点,寻找相连的红色边
for (auto& nextNode : blueGraph[curNode])
{
// 如果 curNode 和 nextNode 相连的红色边未被访问过,访问并加入队列
// 同时需要更新两点之间的最短路径
if (visited[curNode][nextNode][RED] == false)
{
res[nextNode] = min(res[nextNode], step);
// make_pair<nextNode, 0> 的含义是标记当前访问的边为红色,下次应该访问蓝色的
myQue.push(make_pair(nextNode, RED));
visited[curNode][nextNode][RED] = true;
}
}
}
else if (curColor == RED)
{
// 遍历当前节点每一个相邻的节点,寻找相连的蓝色边
for (auto& nextNode : redGraph[curNode])
{
// 如果 curNode 和 nextNode 相连的蓝色边未被访问过,访问并加入队列
// 同时需要更新两点之间的最短路径
if (visited[curNode][nextNode][BLUE] == false)
{
res[nextNode] = min(res[nextNode], step);
// make_pair<nextNode, 1> 的含义是标记当前访问的边为蓝色,下次应该访问红色的
myQue.push(make_pair(nextNode, BLUE));
visited[curNode][nextNode][BLUE] = true;
}
}
}
}
}
// 根据题意,0 到自身的距离为0;在上述操作后,若 0 到其他节点距离仍为INT_MAX,说明不存在符合要求的路径,设置为-1;
res[0] = 0;
for (int i = 0; i < n; i++) if (res[i] == INT_MAX) res[i] = -1;
return res;
}
};
|
从代码可以看出,
- 使用
blueGraph/redGraph保存图中的节点,数据结构是哈希 + vector,哈希的键是节点,值是和该节点直接相连的其他节点;
- 使用
visited三维数组标识节点是否被访问过的信息;
- 使用队列
myQueue保存BFS中的node,这个队列中的元素是<node, expectColor>,即从node出发,从node起始的边的颜色,如果存在这样的边,那么将这条边的终点node和它的下一条不同颜色的边push进队列,循环往复直到所有的边都被访问到为止。
接雨水 II
题目见407. 接雨水 II - 力扣(LeetCode),「待补充」。
参考资料




