疫情居家办公,利用时间好好系统学习下CSAPP,年龄大了,好记性不如烂笔头,写写笔记。
计算机的字长
每一台计算机都有字长,指明指针数据的标称大小,字长决定了的最重要的系统参数是虚拟地址空间的最大大小。
- 字长决定了指针的存储大小,32位的字长的指针存储空间是4字节,64位是8个字节;
- 字长决定了虚拟地址的最大大小,所以32位的寻址空间最大是$2^{32}$Byte = 4GB,64位的是$2^{64}$Byte = 16EB。
典型的C语言的数据类型的大小参考下表
| C声明 | 32bit | 64bit |
|---|---|---|
| char | 1 | 1 |
| short int | 2 | 2 |
| int | 4 | 4 |
| long int | 4 | 8 |
| long long int | 8 | 8 |
| char * | 4 | 8 |
| float | 4 | 4 |
| double | 8 | 8 |
查看上面的表格,32bit和64bit的大部分数据类型的字节长度是一样的,仅有两个不同,long int和char *。可以使用下面的代码查看每个不同类型的字节的大小
|
|
我在自己的64位字长的win10电脑上试了下,除了char *的字节数是4,其他的与上面表格的结果一样。
整数的表示
整数范围
整数分为无符号和有符号整数,如果表示整数$w$位比特,那么无符号表示的范围是$[0, 2^w-1]$,有符号整数表示的范围是$[-2^{w-1},2^{w-1}-1]$。下面是一些典型值,

参考下表,可以在自己的PC上可以通过下面的代码,得到上面的值
| Macro | Value | Description |
|---|---|---|
| CHAR_BIT | 8 | Defines the number of bits in a byte. |
| SCHAR_MIN | -128 | Defines the minimum value for a signed char. |
| SCHAR_MAX | +127 | Defines the maximum value for a signed char. |
| UCHAR_MAX | 255 | Defines the maximum value for an unsigned char. |
| CHAR_MIN | -128 | Defines the minimum value for type char and its value will be equal to SCHAR_MIN if char represents negative values, otherwise zero. |
| CHAR_MAX | +127 | Defines the value for type char and its value will be equal to SCHAR_MAX if char represents negative values, otherwise UCHAR_MAX. |
| MB_LEN_MAX | 16 | Defines the maximum number of bytes in a multi-byte character. |
| SHRT_MIN | -32768 | Defines the minimum value for a short int. |
| SHRT_MAX | +32767 | Defines the maximum value for a short int. |
| USHRT_MAX | 65535 | Defines the maximum value for an unsigned short int. |
| INT_MIN | -2147483648 | Defines the minimum value for an int. |
| INT_MAX | +2147483647 | Defines the maximum value for an int. |
| UINT_MAX | 4294967295 | Defines the maximum value for an unsigned int. |
| LONG_MIN | -9223372036854775808 | Defines the minimum value for a long int. |
| LONG_MAX | +9223372036854775807 | Defines the maximum value for a long int. |
| ULONG_MAX | 18446744073709551615 | Defines the maximum value for an unsigned long int. |
代码如下
|
|
补码表示
$w$bit的有符号整数数学表示如下,
$$ B 2 T_{w}(\vec{x}) \doteq-x_{w-1} 2^{w-1}+\sum_{i=0}^{w-2} x_{i} 2^{i} $$
有一个理解的小技巧,与无符号的整数相比,对于这$w$位bit解读差异仅仅在最高位$x_{w-1}$,有符号数的权重是$-2^{w-1}$,无符号数的权重是$2^{w-1}$。这个是理解书本里面内容的技巧。典型数值的补码表示如下所示,
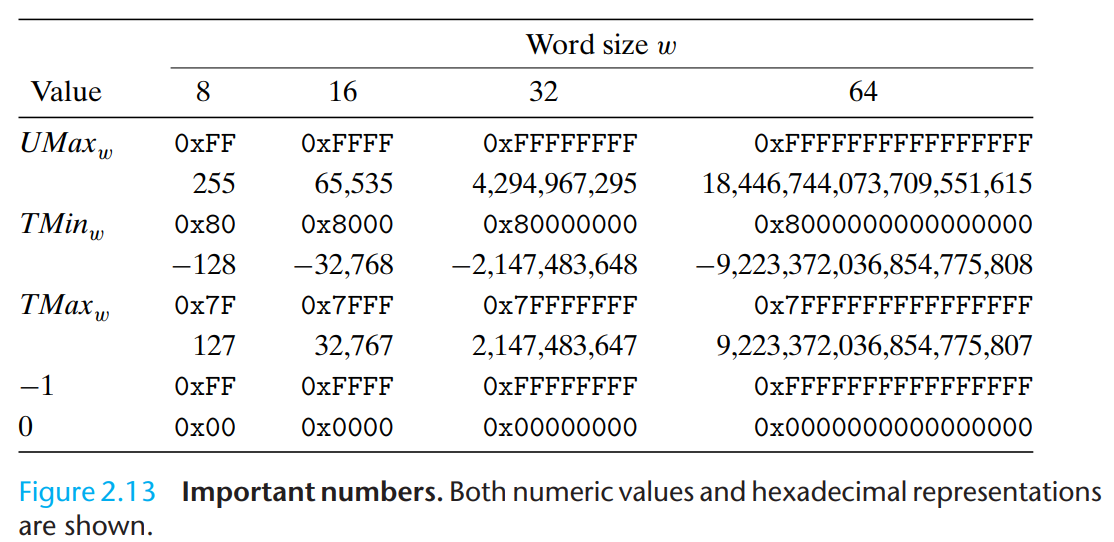
从上面的表格可以看出,
- 相同位宽的无符号整数最大值与有符号整数的-1的底层bit一样;
- $TMin_w = -TMax_w - 1$。
假如
0xFA是某个2字节数的补码表示,那么它实际表示的数字是十进制的多少?
这个问题的解答可以通过补码的定义(参考上文)逐位计算,
$$ B2T_{w}(\vec{x}) \doteq-x_{w-1} 2^{w-1}+\sum_{i=0}^{w-2} x_{i} 2^{i} = -x_{w-1} 2^{w-1}+A $$
但是还有更简单直观的计算方法,我们知道二进制的无符号整数的定义是
$$ B2U_{w}(\vec{x}) \doteq x_{w-1} 2^{w-1}+\sum_{i=0}^{w-2} x_{i} 2^{i} = x_{w-1} 2^{w-1}+A $$
所以,可以得到$B2U_{w}(\vec{x}) = B2T_{w}(\vec{x}) + x_{w-1} 2^{w}$,因此,
- 如果最高位是0,二者的结果是一样的;
- 如果最高位是1,那么可以进一步推导
$$ B2T_{w}(\vec{x}) = B2U_{w}(\vec{x}) - x_{w-1} 2^{w} = -\left[(2^{w} - 1) -B2U_{w}(\vec{x})\right] - 1 $$
而$(2^{w} - 1) -B2U_{w}(\vec{x}) = x按位取反$,所以可以将这个补码的表示理解成unsigned的数,然后减去长度为$w$的全1的二进制比特,再减去1。
所以,0xFA是情况2,补码表示的是 -(~0xFA) - 1 = -0x05 - 1 = -6。
C语言中无符号和有符号的转换
- 位宽一样的无符号和有符号的整数之间的转换,遵循底层的bit不变的原则,互相进行转换,也就是说无论如何转换,仅仅是底层bit的解读方法不同而已。
- C语言中的无符号数和有符号数的二元计算,都会将有符号数强制转换为无符号整数进行计算。
整数的扩展和截断
整数的扩展分为无符号扩展和有符号数的扩展,
- 无符号数的扩展就往高位bit填充0;
- 有符号数的扩展方式是符号扩展,即最高位符号位填充空位。
整数截断逻辑很简单,就是底层的bit表示按照目的的位宽直接截断。这一小节有一个技巧,如果是位宽较小的有符号转换成为位宽较宽的无符号数,则是保持符号不变,先改变位宽,再进行转换,比如下面的代码
|
|
上面的代码中,第2行等价于(unsigned int)(int)sx,先应用符号扩展将short扩展到int,然后再使用等宽bit位的无符号的转换。
编程建议
在实际的软件开发中,尤其要注意无符号整数和有符号整数的转换,比如下面的代码的第4行
|
|
如果length的初始值为0,那么length - 1会是一个非常大的正数,导致对于数组a的越界访问。
整数计算
这一部分的推导看起来比较复杂,刚开始读比较吃力,但是如果看懂了推导中的原则,理解起来就比较清晰了,作者在这一段的推理非常严谨。
整数加法
-
无符号加法很简单,直观来讲,就是逐位相加,超过bit表示范围的高位直接截断。有符号数的加法,推理的原则是有符号数加法补码之和与无符号之和有完全相同的位级表示。
-
对于加法的比较直观的理解,无论是无符号还是有符号数,两个数的加法依然需要在特定位宽的bit位上表示出来,也就是说最终的结果肯定是要落在合理的表示区间的。
- 如果$w$位宽的无符号数超过表示区间,那么就$\mod 2^w$,也就是减去$2^w$;
- 如果$w$位宽的有符号数超过表示区间,同样是$\mod 2^w$,但是分两种,如果是负溢出,就$+2^w$,如果是负溢出就$-2^w$,举例4bit位宽的(-6)+(-3)= -9,小于-8,所以是负溢出,需要再加16,结果就是7。
-
需要注意这里没有整数减法章节,但是介绍了逆元的概念,$x-^t_w{y} = x + (-^t_w{y})$,两个数相减相当于加上第二个数的逆元。计算的原则同上面的2,如果超过表示区间,就做模运算。
-
补码的逆元,有一种比较巧妙的方法,所有比特位取反,然后最低位+1,累进相加。
整数乘法
- 无符号数乘法也很简单,相乘之后取模;
- 有符号数的乘法,推理的原则是有符号数加法补码之积与无符号之积有完全相同的位级表示。所以可以将有符号数的乘法,先转换成为无符号数的乘法计算,之后再以有符号数的补码解读位级表示即可。
- 与常数的乘积可以转化成为右移位、加法和减法的组合,时钟周期比单纯的乘法更少。
整数除法
书里面没有介绍整数的通用除法,详细推理了整数除以2的幂的过程,
- 无论无符号还是有符号整数,$x\gg k = \lfloor {x/2^k}\rfloor$;
- 对于有符号整数,$(x + (1\ll k) - 1)\gg k = \lceil x/2^k\rceil$,这里实际上是一个数学的小技巧,$(m+n-1)/n = \lceil m/n\rceil$。
习题2.44是掌握整数运算的试金石。
浮点数表示
IEEE 754浮点数的表示法
参考浮点数在计算机中的表示。
舍入(Rounding)
上面的IEEE的浮点数的表示方法解决了二进制bit到浮点数的映射问题,但是如果给定一个任意精度的实数$x$,如果使用给定位宽的浮点数表示这个数呢?这里就要引入舍入的概念。舍入解决了将数学上的任意精度的实数集合到计算机表示的有限元素的浮点数集合的映射问题。从之前的浮点数的表示可以看出,计算机表示的浮点数不可能有无限的精度,将半精度浮点数在数轴上标示出来,它在数轴上的分布是离散的,任意两个离散标示值之间的实数是无穷多的,这些实数如果要用半精度表示就只能通过某种方法舍入到标示的某个值上。以下面的问题为例,
半精度浮点数有下面的点,[0.01118, 0.011185, 0.01119],那么0.011183该如何表示成半精度浮点数结果是什么呢?
十进制的舍入
直觉告诉我,这个数要么就是0.01118,要么就是0.011185,因为这个数字介于二者之间,如果按照误差尽量小的原则,那么可以计算一下与两个备选数字的差的绝对值,然后舍入到绝对值最小的那个上。这个就是C语言当前使用的舍入方法,称为最接近值的舍入(round to nearest)。这里面还有一个特殊的地方,以对于十进制的数字为例,舍入到最近的整数,如果这个数是两个整数的中间的值,也就是X.5的形式,那么舍入到最近的偶数。比如0.5是0和1的中间值,它举例两个数的举例是一样的,舍入到0,3.5是3和4的中间值,舍入到4。这样做可以最小化一组数的舍入误差的均值。因此,这种舍入方法又称为round to even。除此之外,还有如下的舍入方法
- 向0舍入,数轴上向着0的方向舍入;
- 向下舍入,也是向$-\infty$舍入;
- 向上舍入,即向$+\infty$舍入
如下图所示,表示了上面的三种情况,

二进制的舍入
那如何将十进制的舍入类推到二进制的舍入呢?这里包括两个步骤:
- 确定舍入的位数,对于某个二进制数$0.001001_{2}$,如果是舍入到小数点后3位,那么这个位数就是3;
- 确定需要舍入的数是否位于两个数的中间位置。
- 如果在中间位置,那么向偶数方向舍入,对于二进制来讲,偶数就是最低有效位为0的数;
- 如果不在中间位置,就向最近的数字舍入。
以上面的数$0.001001_2$为例,就是确认这个数是否在$0.001_2$和$0.010_2$的中间位置,这个位置的数字是$0.0011_2$。很明显$0.001001_2$不是$0.0011_2$,而且小于该值,所以舍入到$0.001_2$。
可以归纳一下,对于给定小数位的浮点数的舍入,对于形如$x.xxxyxxx_2$的二进制数(x和y是0或者1,而且不同位上的数字相互独立),假如舍入到小数点后4位,那么$y=0$或者$y=1$。
- 如果$y=0$,那么可能舍入的两个二进制数是$x.xxx0_{2}$和$x.xxx1_{2}$,两个的中间值是$x.xxx01_2$(逐位相加,左移1个bit);
- 如果$y=1$,那么可能舍入的两个二进制数是$x.xxx1_{2}$和$x.xx(x+1)0_{2}$,两个的中间值是$x.xxx11_2$。
所以,无论要舍入的小数位是0或者1,需要舍入的中间值一定是$x.xxxy1_2$形式。
问题解答
回到最初的问题,$0.01118_{10}$的二进制表示是0010000110111001,按照浮点数的表示法,也就是$1.0110111001_2\times 2^{-7}$,同样的$0.011185_{10}$的二进制表示是0010000110111010,也就是$1.0110111010_2\times 2^{-7}$,如果按照精确到二进制小数点后10位(因为半精度浮点数的尾数是用10个bit来表示的),那么这两个数的中间数应该是$1.01101110011_2\times 2^{-7}$
$0.011183_{10}$,转换成二进制是$1.0110111001110_2 \times 2 ^{-7}$,与中间数的二进制相比,明显大于中间数,所以舍入到比较大的$0.011185_{10}$。如果按照十进制的方式来处理也是一样的,$0.01118_{10}$和$0.011185_{10}$的中间数是$0.0111825_{10}$,明显大于这个中间数,也是舍入到较大的数。
浮点数计算
书本里面没有做详细的计算规则的说明,参考Rounding - CS 357做一下说明。两个浮点数做加法需要完成下面的3个步骤:
- 将两个浮点数调整到相同的指数;
- 做简单的数学的二进制加法;
- 对结果进行舍入。 以二进制数$a =(1.101)_2$和$b=(1.001)_2\times 2^{-1}$为例,假设计算机系统表示尾数的只有3bit,那么计算就会是这样
$$ \begin{aligned} a &=1.101 \times 2^{1} \ b &=0.01001 \times 2^{1} \ a+b &=1.111 \times 2^{1} \end{aligned} $$
最后的结果以小数点后3位作为舍入精度位。可以看到无论是哪个数,有效的数字为是4位,所以没有有效数字位的丢失。
全文完🚀
