二分查找——从入门到精通

最近在准备考试，做了一些二分搜索的题目，感觉有点意思，记录下做题的心得😁。

文章目标

通过阅读本文，可以彻底搞懂二分查找的基本原理及各种变体，可以独立完成下面的力扣题目

力扣题目	考查点
374. 猜数字大小	基本模板
69. x 的平方根	基本模板
278. 第一个错误的版本	查找左边界
153. 寻找旋转排序数组中的最小值	寻找旋转数组中的目标值（无重复元素）
154. 寻找旋转排序数组中的最小值 II	寻找旋转数组中的目标值（包含重复元素）
34. 在排序数组中查找元素的第一个和最后一个位置	查找左右边界

基本原理

在计算机科学中，二分搜索又被成为半区间搜索，对数搜索或者二分chop，它用于在排序数列中找到目标值的位置。算法不断比较数列中间元素与目标值，

如果目标值与中间元素匹配，那直接返回中间的位置；
如果目标值比中间元素小，继续搜索低半边的数列；
如果目标值比中间元素大，那么继续搜索高半边

注意到每次在比较元素之后搜索的区间会减少一半（去掉目标值不可能在的那一半区间），所以在最坏的情况下，算法的复杂度是$O(logn)$。下面是二分搜索与线性搜索的比较示意图，以严格单调增且无重复元素的序列为例，查找目标值为37的序列值。

序列长度是17，

二分查找第一次寻找整个搜索区间的中间的index（从0开始计数）为(0 + 16) / 2 = 8的数字23，23比37小，所以更新查找区间为[9,16]；
查找新区间的中间index = (9 + 16) /2 = 12，结果是数字41，比37大，更新查找区间为[9, 11];
查找新区间的中间index = (9 + 11) / 2 = 10，结果是数字31，比37大，继续更新查找区间为[11, 11]，此时中间元素就是第11号元素，即37，找到目标值，查找结束。

根据以上算法步骤，很顺利就可以写出下面的伪代码，

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// basic template
function binary_search(A, n, T) is
    L := 0
    R := n − 1
    while L ≤ R do
        m := floor((L + R) / 2)
        if A[m] < T then
            L := m + 1
        else if A[m] > T then
            R := m − 1
        else:
            return m
    return unsuccessful

使用上面的基本模板我们就可以解答文章开始列出的第一道题目了，374. 猜数字大小题目，给出二分查找的基本模板。这道题目就是最传统的猜大小的谜题，标准的解答模板的代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


/**
 * Forward declaration of guess API.
 * @param  num   your guess
 * @return 	     -1 if num is lower than the guess number
 *			      1 if num is higher than the guess number
 *               otherwise return 0
 * int guess(int num);
 */

class Solution {
public:
    int guessNumber(int n) {
        int left = 1;
        int right = n;

        while (left <= right) { // detail 1
            int mid = left + ((right - left) >> 1); // detail 2
            int rlt = guess(mid);

            if (rlt == 0) {
                return mid;
            }
			// detail 3
            if (rlt == -1) {
                right = mid - 1;
            }  else {
                left = mid + 1;
            }
        }
        return -1;
    }
};

关键技术细节

Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky – Donald Knuth

就像高德纳所说，二分法的思想简单且易于理解，但是二分法的细节却藏了很多坑，魔鬼就在细节中。为了透彻理解二分法的实现，有必要对上面的代码的下面3个技术细节（标记为detail注释的地方）进行深究。

循环的入口条件

代码16行，为什么循环的入口条件是left <= right？

无论何时$[left, right]$表示可能包含目标值的搜索区间

注意这是个左闭右闭的闭区间，单纯从数学角度出发，这个区间最短的长度就是1，也就是$left = right$的时候。如果$left > right$了，那$[left, right]$就是空集，这个集合肯定不包含目标值，也就没有继续搜索的必要了，所以循环退出。

中点计算

为什么是mid = left + ((right - left) >> 1)，也就是数学的$floor((left + right) / 2)$? 这里的中点转换成数学表示就是 $$ \begin{align} mid = \left \lfloor\frac{left + right}{2} \right \rfloor \end{align} $$ 其实，我们还有另外一种选择，将中间值定为 $$ \begin{align} mid = \left \lceil\frac{left + right}{2} \right \rceil \end{align} $$ 第2种方式的中点值的选择是否可行？从后面的分析，**其实是可行的。**那这两个计算公式有什么区别？最大的区别在于$right = left + 1$的时候，也就是搜索区间长度为2左右端点挨着的时候，如下图所示，下一次循环计算mid，第1个公式结果是$mid = 4$，而第2个公式的结果是$mid = 5$，

指针相邻

，第1个公式$mid = \left \lfloor\frac{left + right}{2} \right \rfloor = \left \lfloor\frac{left + left + 1}{2} \right \rfloor = left$，而第2个公式$mid = \left \lceil\frac{left + right}{2} \right \rceil = \left \lceil\frac{left + left + 1}{2} \right \rceil = left + \lceil 0.5\rceil = left + 1 = right$，请记住这个重要的结论。

当搜索区间的左右两端点挨着的时候（即$right = left + 1)$，floor函数计算的中点mid是left，ceil函数计算的中点mid是right

请记住这个特殊的区间情况，至于为何基础模板选择floor而没有选择ceil，在后面的变化类型一节很关键。

搜索区间调整

在每次判断与target的差距之后，搜索区间为什么是这么调整的？二分法另一个容易搞错的问题是区间调整，$left$和$right$好像可以选择$mid$的3个边界值$mid, mid - 1, mid + 1$中的任意一个，其实调整的原则很简单，

排除target不可能存在的区间，保留可能存在的区间

保证任意判断分支为true时最后都可以跳出循环，尤其当$right = left + 1$时

先看第1条原则，基础模板中，根据mid的值与目标值的差距，搜索区间$[left, right]$的调整有3个判断分支：

如果和目标值相同$A[mid] = A[target]$，直接跳出循环，返回mid(代码第21行)；
如果比目标值大$A[mid] > A[target]$，那么肯定$target < mid$，所以$target \le mid - 1$，因此$target$位于区间$[left, mid - 1]$上，更新$right = mid - 1$；
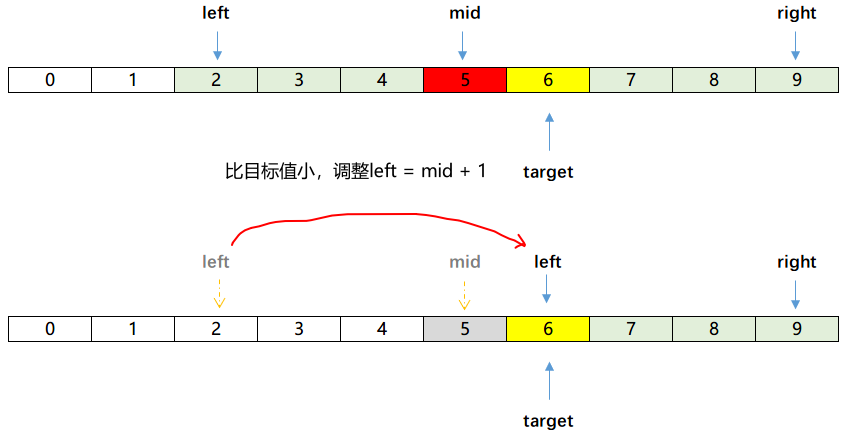
如果比目标值小$A[mid] < A[target]$，那么肯定$target > mid$，所以$target \ge mid + 1$，因此$target$位于区间$[mid + 1， right]$上更新$left = mid + 1$。

区间的调整仅仅保留了$target$可能存在的部分。

分支3的调整情况，看如下图示

考察第2条原则，是否可以退出循环？这个循环的退出条件是$left > right$。对照上面的3个判断分支分别为true的情况：

第1个判断分支直接退出循环，符合条件；
同理，第2个判断分支每次判断之后$right$在变小，所以必然在若干次之后比$left$小，直至退出循环
第3个判断分支每次调整之后$left$在变大，所以所以必然在若干次之后比$right$大，直至退出循环

所以随着区间的调整，必然会在某一步满足退出的条件。特别的，当$right = left + 1$时，$mid = left$；

第2个判断分支，$right = mid - 1 = left - 1 = right - 2 < left = right - 1$，跳出循环
第3个判断分支，$left = mid + 1 = left + 1 = right$，再次进入循环，此时$mid = left = right$，$left = mid + 1 = right + 1 > right$，可以看到在迭代2次之后也退出循环

第2条原则满足。

结合上面的分析，二分法的步骤包括：

从$A[mid]$与$target$的大小判断入手，判断它们的各种大小关系分支，确定每个判断分支的区间调整策略，需要满足下面的两条原则

排除target不可能存在的区间，保留可能存在的区间

保证任意判断分支为true时最后都可以跳出循环，尤其当$right = left + 1$时

深入探究

上一小节讨论了3个关键技术细节，循环入口条件、中点计算和搜索区间调整，下面可以看到在满足上面的原则基础上，它们都可以变化。

分支合并

当前的基础代码有3个判断分支，是否可以将3个分支合并成2个呢？下面的基础模板就可以。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution {
public:
    int guessNumber(int n) {
        int left = 1;
        int right = n;

        while (left < right) { // 退出条件变了
            int mid = left + ((right - left) >> 1);
            // 调整策略的分支从3个变成了2个
            if (guess(mid) <= 0) {
                right = mid;
            }
            else {
                left = mid + 1;
            }
        }
		// 返回的条件也变了
        if (guess(left) == 0) {
            return left;
        }

        return -1;
    }
};

再仔细考察一下，上面的代码，3个地方发生变化（已经在注释种标出）依然可以通过测试，其实还是按照上面的2个原则来看。

每次调整区间，排除target不可能存在的区间，保留可能存在的区间

重新分析之前的3个判断分支，比较特殊是第1点，如果$A[mid] = A[target]$，那么$mid = target$，很明显

判断分支1与判断分支2合并，当$A[mid] \ge A[target]$，$target \le mid$，所以$target$可能位于$[left, mid]$区间，调整$right = mid$，注意此处$right \ne mid -1$
判断分支1与判断分支3合并，当$A[mid] \le A[target]$，$target \ge mid$，所以$target$可能位于$[mid, right]$区间，调整$left = mid$，注意此处$left \ne mid +1$

这两个策略看起来似乎都可以，结合其他两种情况，如果将3个分支合并为2个，应该有2种调整策略

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


# solution 1，另一种正确的方案
function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L < R do
        m := floor((L + R) / 2)
        if A[m] >= T then
            R := m
        else:
            L := m + 1
    if A[L] = T then
        return L
    return unsuccessful

或者

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


# solution 2，错误示范
function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L < R do
        m := floor((L + R) / 2)
        if A[m] <= T then
            L := m
        else:
            R := m - 1
    if A[L] = T then
        return L
    return unsuccessful

保证任意判断分支为true时最后都可以跳出循环，尤其当$right = left + 1$时

我们再看上面的两种伪代码，退出的条件是$left >= right$，直接考察$left = right -1$的情况，如果在搜索的若干步之后搜索的区间变成下面的情况

下一步搜索的$mid = 4$，按照方案2，如果此时
1. 第2个判断分支为true，$right = mid - 1 = 3 < left$，退出循环；
2. 第1个判断分支为true（代码第7~8行），那么调整$left = mid = 4$，再次进入之后会发现陷入死循环，核心原因在于中点的选择上，因为使用的是floor函数，导致left永远恒等于mid，换句或说，$left$永远不再增加，而且也进不到更新$right$的分支，陷入死循环，考察方案1就没有这种情况。
所以方案2的结果是错的。

中点计算变更

上面的方案2，因为不满足第2条原则而失败，那有没有办法通过改变其他部分而满足原则呢？第1个判断分支如果为true，当$right = left + 1$时，根据代码第6行，$mid = left$，所以进入分支之后$left = mid = left$，那可以将第6行的代码改成下面这样，

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


# solution 3，solution 2的改造
function binary_search_alternative(A, n, T) is
    L := 0
    R := n − 1
    while L < R do
        m := ceil((L + R) / 2) # ceil取代floor函数
        if A[m] <= T then
            L := m
        else:
            R := m - 1
    if A[L] = T then
        return L
    return unsuccessful

再考察一下上面的搜索区间左右端点相邻的情况，下一次搜索的$mid = 5$，无论走哪一个判断分支，最终$left = right$，跳出循环，所以对于第2条原则需要补充

可以通过调整中点的计算方式，满足原则2，从而避免死循环

判断条件变更

需要注意，其他2个的模板的循环条件为$left < right$，当$left \ge right$时退出，如果$left = right$，那么搜索的区间只剩下一个元素，跳出循环之后别忘了要检查这个元素是否满足条件。如果最后的这个元素依然不是target，那么所有的元素也不是了，所以在最后我们加了一个判断，

1
2
3


    if A[L] = T then
        return L
    return unsuccessful

变种题目

理解上面的分析过程之后，进入进阶版的二分法题目。

重复元素左边界

参考278. 第一个错误的版本，从某个版本开始，版本就已经不可用了，但是在这个版本之前，所有的版本均可用，需要找出第一个不可用的版本。假如说，我们有100个版本，从第70个版本开始不用，那么怎么快速找到70呢？如下所示

题目要找到最左边第一个true对应的下标70，也是找到重复的true区间的左边界。初始化$left = 0, right = 100$，我们还是从判断分支入手，

如果$A[mid] = true$，那么$target$可能位于$[mid + 1, right]$区间，调整$left = mid + 1$；
如果$A[mid] = false$，$mid$可能是$target$，但是$mid + 1$不会是$target$（因为我们要找的是最左边的那个FALSE），那么$target$可能位于$[left, mid]$区间，调整$right = mid$

结合中点的计算原则$mid = floor((left + right)/ 2)$，判断$right = left + 1$时候，2个判断分支最终都可以跳出循环。最终代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


// The API isBadVersion is defined for you.
// bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        int left = 1;
        int right = n;

        while (left < right) {
            mid = left + ((right - left) >> 1);
            if (isBadVersion(mid) == false) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        return left;
    }
};

更一般的，假如我们要查找序列$[1,2,3,4,4,5,6,6,7,7,9,10,10,10]$中的最左边的10的index，该如何处理？从分支判断入手，

如果$A[mid] \lt 10$，那么10可能位于区间$[mid + 1, right]$区间，调整$left = mid + 1$；
如果$A[mid] = 10$，那么10可能位于区间$[left, mid]$区间，调整$right = mid$；
如果$A[mid] \gt 10$，那么10可能位于区间$[left, mid - 1]$区间，调整$right = mid - 1$

合并分支2和分支3，变成

如果$A[mid] \lt 10$，那么10可能位于区间$[mid + 1, right]$区间，调整$left = mid + 1$；
如果$A[mid] \ge 10$，那么10可能位于区间$[left, mid]$区间，调整$right = mid$

判断当$left = right - 1$时，两个分支都可以顺利退出。代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    int CheckVal(int n) {
        int left = 1;
        int right = n;

        while (left < right) {
            mid = left + ((right - left) >> 1);
            if (A[mid] < 10) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        if (A[left] == 10) {
            return left;
        }
        return -1;
    }
};

重复元素右边界

假如我们要查找序列$[1,2,3,4,4,5,6,6,7,7,9,10,10,10]$中的最右边的10的index，该如何处理？从分支判断入手，

如果$A[mid] \lt 10$，那么最右边的10可能位于区间$[mid + 1, right]$区间，调整$left = mid + 1$；
如果$A[mid] = 10$，这个$A[mid]$可能是最右边的10，也可能不是，但是$A[mid - 1]$肯定不是最右边的10了，所以目标值可能位于区间$[mid, right]$区间，调整$left = mid$；
如果$A[mid] \gt 10$，那么最右边的10可能位于区间$[left, mid - 1]$区间，调整$right = mid - 1$

合并分支1和分支2，变成

如果$A[mid] \le 10$，那么10可能位于区间$[mid, right]$区间，调整$left = mid$；
如果$A[mid] \gt 10$，那么10可能位于区间$[left, mid - 1]$区间，调整$right = mid - 1$

判断当$left = right - 1$时，按照floor函数计算，第1个分支会陷入死循环，所以需要调整中点的计算方式为ceil，判断两个分支都可以顺利退出，所以代码如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    int CheckVal(int n) {
        int left = 1;
        int right = n;

        while (left < right) {
            mid = left + ((right - left) >> 1) + 1;
            if (A[mid] <= 10) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        if (A[left] == 10) {
            return left;
        }
        return -1;
    }
};

旋转数组（无重复元素）

来做文章目标中的153. 寻找旋转排序数组中的最小值这道题，具体看看示例2中的题目怎么做

示例2

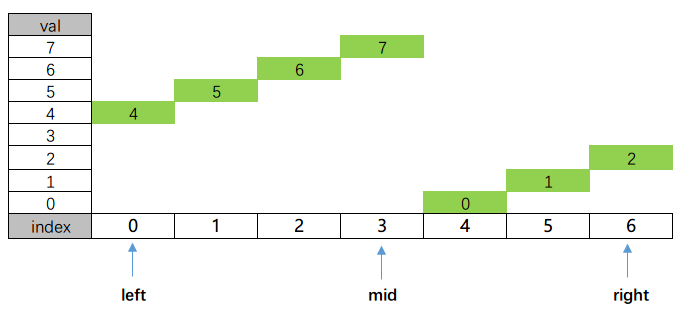
具体的值和index的分布如下所示

初始化搜索范围，$left = 0, right = n - 1 = 6$；
$mid = 3$，从判断$A[3] = 7$与$target$的值入手，但是比较棘手的是$target$是多少呢（我们不知道最小值是0，仅仅知道这是一个旋转序列）？那我们根据什么判断$target$存在的可能区间呢？注意下面这幅图

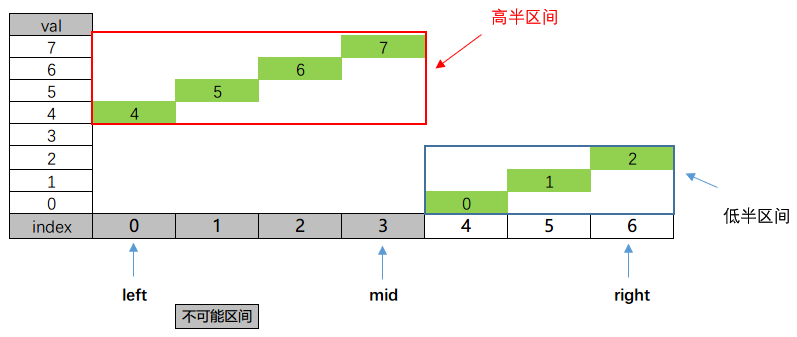
这个旋转数组分为前后两个区间，前面区间每一个数字都比后面区间的数字大（因为没有重复数字），分别称为高半区间和低半区间。很明显，

最小值一定在低半区间，且位于低半区间的起始点上；
我们不知道低半区间的起始点在哪里，也不知道高半区间的终点在哪里；
我们可以根据当前元素与数组最后一个元素（想想为什么不是第一个元素）的大小确认出具体位于哪个半区间，如果$A[id] > A[n - 1]$，那么在高半区间，否则在低半区间。

那这个和判断$target$所在区间有什么关系呢？如果$mid$位于高半区间，那么可以肯定最小值肯定不在$[left, mid]$中，更新$left = mid + 1$，如果位于低半区间，可以肯定$[mid+ 1, right]$不可能是最小值，更新$right = mid$。于是有下面的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution {
public:
    int findMin(vector<int>& nums) {
        if (nums.size() == 1) return nums[0];
        int left = 0;
        int right = nums.size() - 1;
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] > nums[nums.size() - 1]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return nums[left];
    }
};

判断是否在$right = left +1$时，每个分支可以跳出循环，可以👍，完毕。

旋转数组（包含重复元素）左边界

再来看154. 寻找旋转排序数组中的最小值 II - 力扣（LeetCode），这个题目与上面有点区别，就是它有重复元素，如下图

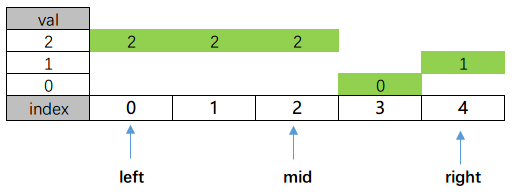
看起来可以按照上面的题目如法炮制，判断$A[mid]$与$A[n -1]$的大小，

如果$A[mid] > A[n -1]$，$mid$位于高半区间，则最小值肯定不在$[left, mid]$里面，更新$left = mid + 1$；
如果$A[mid] < A[n -1]$，$mid$位于低半区间，则最小值肯定不在$[mid +1, right]$里面，更新$right = mid$；
如果$A[mid] = A[n-1]$，这个时候就说不清楚$mid$是在高区间还是低区间了。因为可能有下面的情况

再仔细想想，其实在这一步，我们不需要知道我们位于哪个区间，我们要清楚$mid$跟最小值的index的关系，参考下面的图

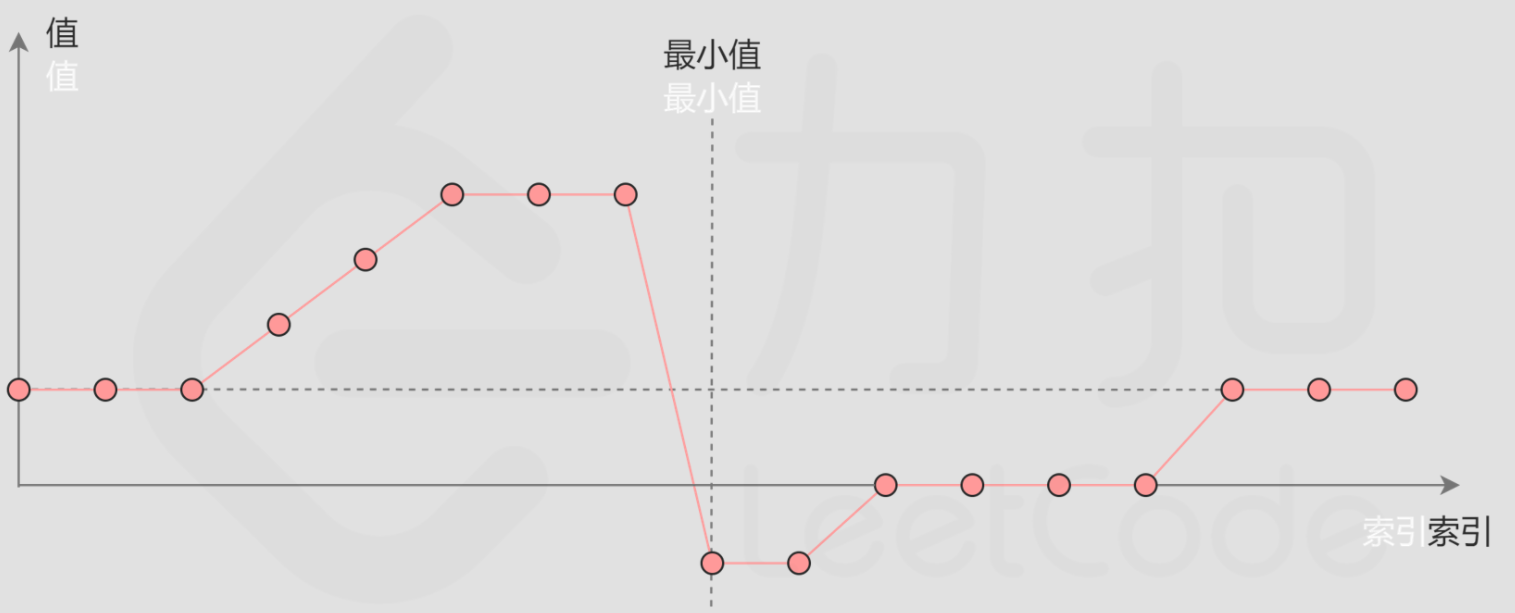
考虑数组中的最后一个元素$A[right]$，在最小值右侧的元素，它们的值一定都小于等于$A[right]$；而在最小值左侧的元素，它们的值一定都大于等于 $A[right]$。假定中点为$pilot$，比较$A[pilot]$与$A[right]$的大小，可以间接判断出$pilot$和$target$的位置关系。

第一种情况，$A[pilot]<A[high]$，说明此时最小的点位于$pilot$的左边，所以更新$right = pilot$；

第二种情况，$A[pilot]>A[high]$，说明此时最小的点位于$pilot$的右边，所以更新$left = pilot + 1$；

第三种情况，$A[pilot]=A[high]$，此时唯一可以确定的是最小值在$high$的左边，所以更新$right = right - 1$

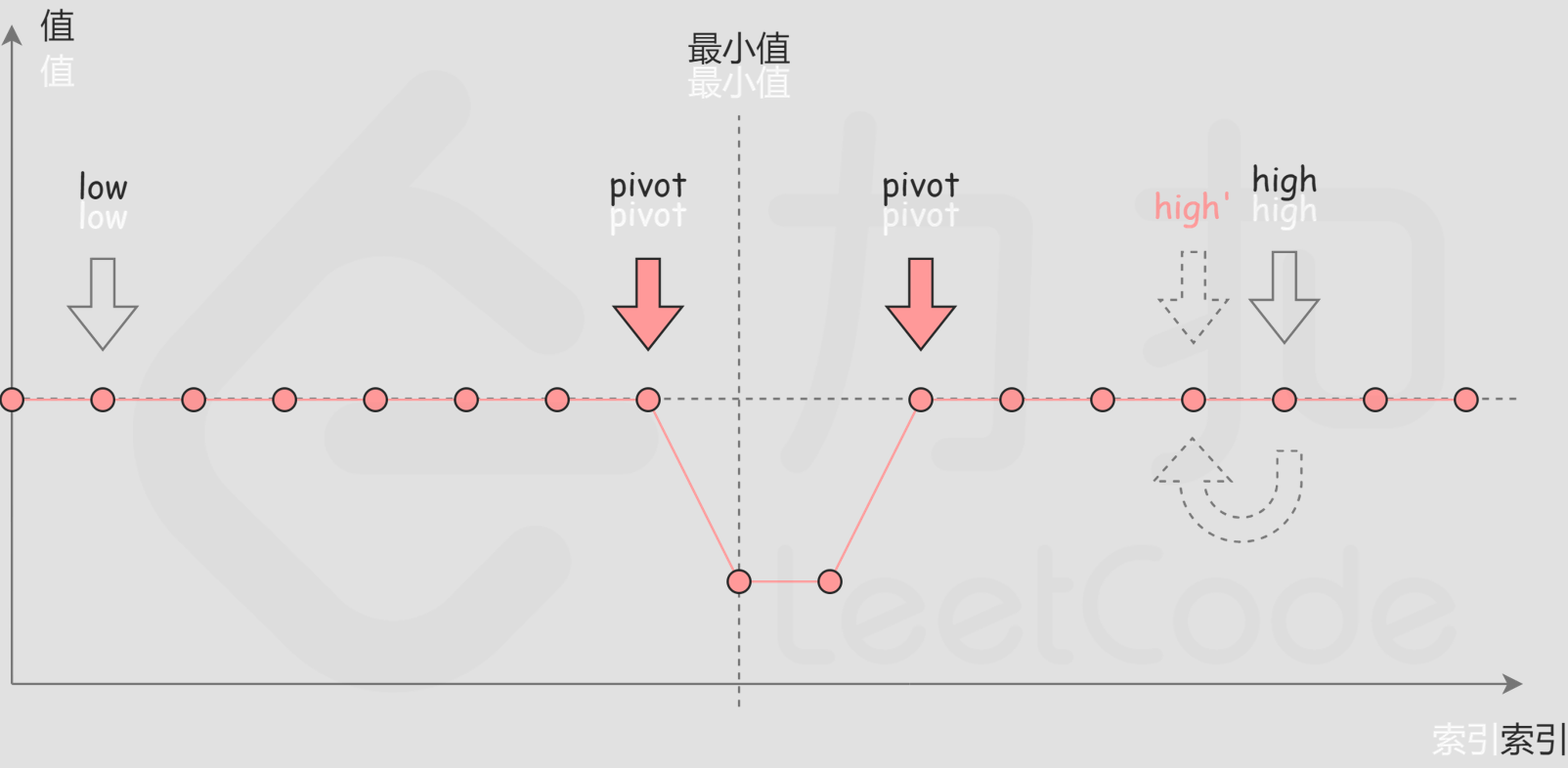
则有如下的答案

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    int findMin(vector<int>& nums) {
        int low = 0;
        int high = nums.size() - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            }
            else if (nums[pivot] > nums[high]) {
                low = pivot + 1;
            }
            else {
                high -= 1;
            }
        }
        return nums[low];
    }
};