补码是如何产生的？

今天读《数值分析》第 0 章的实数的浮点表示，对计算机存储数据的机制产生兴趣，所以自己写了个小程序结合现有资料探索总结下。

我们现在遇到一个计算机的基本问题，

给定一个数（整数或者实数）$X$，如何以 $w$个比特位的形式$[x_{w-1},x_{w-2},…,x_0]$将它存储在计算机的内存里？

程序结果

我自己写的 C 程序如下，分别打印出整数120055,-411，浮点数102.3235， -3.256和双精度浮点数120.254， -56.2441在计算机内存中的二进制比特，这几个数字是我随手写的，但是均没有超出计算机的表示范围。程序如下所示

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<stdio.h>
#include<stdlib.h>

typedef enum
{
    INT = 4, //int和float有4个字节
    FLOAT = 4,
    DOUBLE = 8 //double有8个字节
} TYPE_E;

void showBytes(unsigned char *ch, TYPE_E len)
{
    int i;

    for(i = 0; i < len; i++)
    {
        printf(" %.2x", ch[i]);
    }
    printf("\n");
}

int main(int argc, char *argv[])
{
    int a = 120055, b = -411;
    float a_f = 102.3235, b_f = -3.256;
    double a_d = 120.254, b_d = -56.2441;

    printf("binary of a %d, 0x", a);
    showBytes((unsigned char*)&a, INT);
    printf("binary of b %d, 0x", b);
    showBytes((unsigned char*)&b, INT);
    printf("binary of a_f %f, 0x", a_f);
    showBytes((unsigned char*)&a_f, FLOAT);
    printf("binary of b_f %f, 0x", b_f);
    showBytes((unsigned char*)&b_f, FLOAT);
    printf("binary of a_d %f, 0x", a_d);
    showBytes((unsigned char*)&a_d, DOUBLE);
    printf("binary of b_d %f, 0x", b_d);
    showBytes((unsigned char*)&b_d, DOUBLE);

    getchar();

    return 0;
}

程序运行完成之后的结果如下所示

因为是小端存储，因此整理之后的结果如下所示

从上面的结果可以看出不同数值的长度不同，因为计算机给每个不同的类型分配的内存大小不同，这个可以通过 C 中的sizeof函数看出来。下面我们需要搞清楚的是，**为什么这些数都是以这样的形式和内容存储在计算机中的？**这一篇文章，我们先谈比较简单的整数的表示，下一篇文章会解释浮点数的表示方法。

编码机制

二进制表示

我们知道，计算机中以二进制的形式存储数字，所有的十进制的数字都需要转换成二进制存储起来。至于十进制和二进制如何转换，课本和网上已经有非常详尽的解释（可参考文末的文章），而且有非常完善的在线进制转换工具可以轻松实现多个进制之间的相互转换，这里不再赘述。为了便于对比，除非特殊情况，本文的内容均使用十六进制数。

整数编码

我们先从简单的正整数入手，120055 = 0x1D4F7，考虑到计算机int类型使用 4 个字节，补齐前面的0，于是为0x0001D4F7，这个与我们程序验证结果一致。因此，可以断定正整数在计算机中存储的形式就是它转换成二进制的形式。

引入负数

那么负整数是如何保存的呢？来看第二个数字-411，因为411 = 0x19b，所以我们直观的表示就是-0x19b，但是计算机不能表示负号，那么该如何处理这个问题呢？一个直接简单的想法是使用 1 个比特表示符号正负，自然的想法是取最高位，0 表示正数，1 表示负数，所以可以表示成0x8000019b。这样表示比较直观，但是有一个小问题。为了便于说明，我将问题的规模缩小，比如考虑 3 个比特的二进制和十进制数之间的转换。如果使用我们之前的换算方法，那么二进制编码的情况如下

很明显，十进制0有两种不同的编码方式，3 个比特本来可以表示不同的 8 个数，却只能表示 7 个不同的数，这是对信息比特的浪费。最佳的表示方式应该满足，在一个一致的运算关系之下，不同的二进制编码表示不同的十进制数，于是引入了补码的概念。

补码

首先，补码如何计算？

给定 $w$ 个比特，如何求一个十进制数 $X$ 的二进制补码 $[x_{w-1},x_{w-2},…,x_0]$？

以 8 比特为例，如果求正整数 8 的相反数，我们用0-8 = -8，补码的取法类似，使用如下的计算

００００００００ －００００１０００ －－－－－－－－－ 　１１１１１０００

但是不够减，小学算术告诉我们可以向前借位，于是有

１００００００００ －００００１０００ －－－－－－－－－ 　１１１１１０００

问题解决，总结下这个变换过程：最高有效位表示正负号，正数 XX 的补码是其自身的二进制表示 XX，负数 XX 的补码是 2w−|X|2w−|X|。

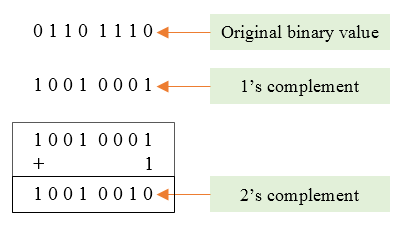
举个例子，比如使用 4 个 bit 表示 6 和 - 7 的补码，分别是 $(1100)2$和和$(2^4 - |7|){10} = (9)_{10} = (1001)_2$。这里需要特别说明下，经常听到求一个负数。这里需要特别说明下，经常听到求一个负数X的二进制补码，就是先求的二进制补码，就是先求$|X|$ 的二进制表示，除了符号位之外的所有位取反加 1，这和上面的方法等效，因为$2^w - |X| = (1000…0)_2 - |X| = (111…1 + 000…1)_2 - |X| = (111…1)_2 - |X| + 1$，一目了然。使用该方法编码 3 个比特的编码，如下所示

很明显，使用补码，所有的十进制数都有与之对应唯一的二进制编码表示。使用这个方法可以计算出来 $(-411){10} = (FFFFE65){16}$，与之前程序的结果完全一致！！于是猜想计算机使用补码存储对应的整数！

已知一个 $w$ 比特的二进制补码$[x_{w-1},x_{w-2},…,x_0]$，如何求它对应的十进制数 $X$？

如果知道这个数的补码形式，根据《深入理解计算机系统》中给出二进制数补码表示$[x_{w-1},x_{w-2},…,x_0]$ 与十进制数之间的转换关系

$$ X = -x_{w-1}2^{w-1} + \sum_{i = 0}^{w-2}{x_i2_i} $$

使用补码有什么好处？

第一，0的表示唯一。 第二，所有整数的加法统一在一个法则之下，使用一套逻辑电路。现在有一个问题，异号两个数相加怎么计算，比如

1 + (-3) = ?

根据数字的表示不同，这个问题有如下几种解法。

• 十进制解法，也就是我们人类自己的解法，首先我们会判断 3 和 - 2 那个绝对值大，之后符号取绝对值大的那个，最后绝对值大的减去绝对值小的作为新的数字的绝对值。听起来比较拗口，这里分了好几个步骤：1) 比较绝对值大小，决定符号；2) 绝对值相减确定结果的绝对值。

• 使用之前的编码方案（为了简单，我们仍然使用 3 比特数举例，如果我们使用之前的表示方法），直接二进制相减，即 $(1 + (-3))_{10} = (001 + 111)_2 = (000)2 = (0){10}$，这是明显错误的结果。如果想要正确，我们需要借鉴十进制的解法，先判断绝对值，再确定符号，两个数字相加需要将符号单独拎出来处理，加法是计算机的最基础的运算操作，这样的处理逻辑增加了电路的设计复杂度，极大地影响计算机的性能。

• 使用补码。$(1 + (-3))_{10} = (001 + 101)_2 = (110)2 = (-2){10}$，可以自行验证其他的所有的异号的和，都能得到正确的答案。可以看出，符号位直接当作数据的一部分参与运算，计算机并没有单独对其做处理，从计算机的角度来看简单粗暴有效，之所以会有这么神奇的结果，是因为 $$ [X]_补 + [Y]_补 = [X+Y]_补 $$ 这个定理可以按照两数同号，两数异号两种情况进行证明。正因为有这样的数学关系，所以计算机将补码作为整数存储的形式。

参考资料

• 《数值分析》，0.2 和 0.3 节
• 《深入理解计算机系统》，第二章
• 二、八、十、十六进制转换（图解篇） - 听风吹雨 - 博客园
• 关于 2 的补码
• Two’s Complement